Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 프로젝트
- 2차프로젝트
- JSP/Servlet
- KNN모델
- intent
- gitclone
- MSE
- 선형모델 분류
- 활성화함수
- 국비지원
- 교차검증
- 백엔드
- 오픈소스깃허브사용
- randomForest
- 2차 실전프로젝트
- semantic_segmentation
- 취업연계
- 1차프로젝트
- MVCmodel
- 안드로이드
- 크롤링
- 스마트인재개발원
- ERD
- 취업성공패키지
- springSTS
- 하이퍼파라미터튜닝
- 손실함수
- 비스포크시네마
- 머신러닝
- 내일배움카드
Archives
- Today
- Total
또자의 코딩교실
[스마트 인재개발원] Linear Model(선형 회귀모델)과 선형모델 평가요소 본문

선형모델 : 데이터를 선형 함수로 구분하는 모델.
학습에서 나온 선형함수로 새로운 데이터를 예측함
✅ 작동방식
입력 특성에 대한 선형 함수를 만들어 예측을 수행함
선형모델은 분류와 회귀문제 모두 해결 가능함
- 분류 : 정답으로 사용할 수 있는 label이 정해져 있음. (=정해진 정답의 종류 중에서 하나를 예측)
- 회귀 : 정답으로 사용할 수 있는 label이 정해져 있지 않음. (=정답으로 삼을 수 있는 종류가 엄청나게 많으며 주로 숫자를 예측함.)
✅ 장단점
결과 예측(추론)속도가 빠르다.
대용량 데이터에도 충분히 활용 가능하다.
특성이 많은 데이터 세트라면 훌륭한 성능을 낼 수 있다.
특성이 적은 저 차원 데이터에서는 다른 모델의 일반화 성능이 더 좋을 수 있다. >> 특성확장 필요
과대적합되기 쉽다. (LinearRegression Model은 복잡도를 제어할 방법이 없기 때문) >> 모델 정규화 필요
✅ 손실함수(선형 모델 평가 요소)
- 입력한 데이터를 잘 포함하는가?
- 비용함수의 오차가 얼마나 낮은가? >> MSE를 보고 판단

비용함수 그래프 - MSE란? : 평균제곱오차. 실제값과 예측값간의 관계를 나타냄.
- MSE가 최소가 되는 w와 b를 찾는 방법
- 수학 공식을 이용한 해석적 방법 (=Linear Regression)
(= '주어진 특성과 결정 값 데이터에 기반하여, 학습을 통해 최적의 회귀계수(W,b)를 찾아내는 것',
선형 회귀 모델에서 최적의 모델 = 기존 데이터와의 점과 오차(사이 거리)가 크지 않은 선)
- 경사하강법 (=GDA, Graidient Descent Algorithm)
(= 비용함수의 경사를 구하여 learning_rate 만큼 극값으로 계속 이동하여 값을 최적화하는 방법,
SGDRegressor 모델의 작동원리)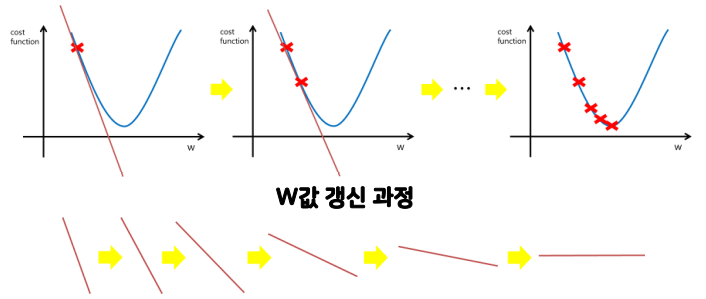
- 수학 공식을 이용한 해석적 방법 (=Linear Regression)
아래에는 선형모델의 평가요소에 대한 세부적인 설명이다. 세부적인 수학적인 원리는 이 포스팅에서 알아보지 않는다.
✅ 평균 제곱오차 (MSE) = 모든 오차들을 제곱해서 평균 낸 값
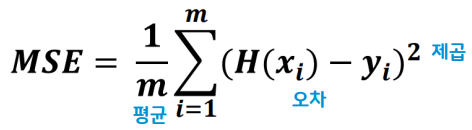
- 데이터의 모든 오차(H(x)에서 ymodel값을 뺀 값.)들을 모두 더해준다.
오차가 0에 수렴하는 것을 막기 위해 제곱값인 H(x)으로 만들어 음수값을 없애준다. - 그 후 m개로 나눠 평균을 구함
- 가장 MSE가 낮을때의 W와 b가 나오는 모델이 적합한 선형모델
✅ 평균 제곱근 오차 (RMSE)

- MSE에 루트만 씌워 원래 단위로 맞춰주고자 사용하게 됨.
- MSE의 단점 (제곱값인 H(x)을 썼더니 원래 쓰던 단위값이 아닌 뻥튀기된 값이 됨) 을 극복하기 위해 제안됨
- RMSE/MSE는 예측 대상의 크기에 영향을 받는다는 단점이 있다. (좀 더 공부해볼것)
✅ 교차 엔트로피 오차 (RMSE)
- 0과 1일 확률 두개를 검토하여 어느쪽이 더 많은가 판단
교차 엔트로피 오차는 더 작은 값일수록 정답이 가능성이 높다고 판단한다.

log는 밑이 e인 자연로그이다.
y:신경망의 출력, t:정답레이블 (원-핫 인코딩)
✅ Logistic Regression 선형 회귀 모델

- Sigmoid 함수를 사용하는 Logistic Regression(선형 회귀)모델.
직선이었던 함수는 Sigmoid 함수를 만나 S자형태의 곡선으로 됨 - 최종 결과는 예측값
- 가중치값이 낮을수록 해당하는 특성은 작은 영향을 미치는 속성이 됨
(= 가중치가 0이라면 주는 영향이 거의 없다) - 선과 점의 거리가 가깝다
(= 예측값과 원래 데이터값이 차이가 별로 없음)
(= 정확도 상승) - 선형 회귀 모델에서 오차 : 제곱 값 사용 (원래 값을 뺄셈할 때, 절댓값을 사용하기 위함)
- 어떤 위치에 선을 긋느냐에 따라 y값은 달라질 수 있음
- 가중치값이 높을수록 해당하는 특성은 크게 영향을 미치는 속성이 됨
✅ Sigmoid 함수 = 이진분류에서 굉장히 효율이 좋은 분류기준

- 가장자리에 있는 데이터들을 직선 형태의 데이터보다 효과적으로 이상치들을 처리할 수 있음.
- 중간의 0.5를 기준으로 플러스마이너스 일정구간의 데이터들을 얼마나 잘 분류하나가 관건임.
- x가 양 극단으로 발산해도 0 이하나 1 미만으로 떨어지지 않고 범위내에서 처리될 수 있음.
- 분류에 능함. = 0.5를 기준으로 이상이면 1, 이하면 0으로 분류
- 규제 : C(alpha의 역수)로 제어
- 알파값이 크면 규제강도가 커짐. 규제강도가 커지면 가중치가 줄어듬.
- C 는 알파의 역수이므로 C값이 커질수록 규제강도가 작아지고 작아지면 규제강도가 늘어남.
✅ 모델 정규화 (손실함수 규제법)

- LinearRegression Model은 복잡도를 제어할 방법이 없어 과대적합 되기 쉽다. >> 정규화 사용
- 정규화에 사용하는 L1, L2규제
- 란다를 사용해 규제강도를 제어함
- L1 : Lasso
다 같은 힘으로 눌러버려 특정 계수는 0이 됨. >> 변수선택 가능
mse와 유사함
변수간 상관관계가 높으면 성능이 떨어진다. - L2 : Ridge
모든 원소에 골고루 규제를 적용해 0에 가깝게 함
변수간 상관관계가 높아도 좋은 성능을 가진다.
- 1일 확률과 0일 확률을 둘다 검토한다.
- 교차 엔트로피 오차함수
- 0과 1일 확률 두개를 검토하여 어느쪽이 더 많은가 판단
- 주요 매개변수 (Hyperparameter)
- α
C. (=1/alpha) - 규제항을 추가하여 과대적합을 방지
- 값이 작을수록 규제가 강해짐
- α
- 기본적으로 L2규제를 사용하고 중요한 특성이 몇 개 없다면 L1규제를 사용해도 무방

모델 선택 기준
✅ SGDRegressor 모델
- 경사하강법 이용
- SGDRegressor(max_iter, eta0)
- 가중치 업데이트 횟수 : max_iter
- 학습률(learning_rate) : eta0
from sklearn.linear_model import SGDRegressor
#ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
#모델 생성 및 파라미터 조정
sgd_regressor = SGDRegressor(max_iter=5000, #가중치 업데이트 반복 횟수(epoch)
eta0 = 0.001, #학습률(learning rate)
verbose = 1) #학습과정을 확인(fit명령어 실행시 가중치 업데이트 사항 반영)
#ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
#모델 학습 및 예측
sgd_regressor.fit(X, y)
#예측값
sgd_regressor.predict([[1.3]])
#실행결과
array([14.0512276])
#ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
#가중치
sgd_regressor.coef_
#실행결과
array([9.79478687])
#ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
#절편 = 오차가 제일 작은 지점
sgd_regressor.intercept_
#실행결과
array([1.31800467])✅ GridSearch
- 매개변수들의 가능한 모든 조합을 시도하고 가장 좋은 조합을 찾는 방법
from sklearn.model_selection import GridSearchCV
#CV = Cross Validation : 교차검증까지해서 가장 좋은 조합을 찾아줌
#딕셔너리{파라미터 : 조합}
params = {'max_depth':[3,5,7],
'max_leaf_nodes' : [4,6,8],
'min_samples_split':[4,6,8]}
#총 27가지의 조합
#GridSearchCV (모델, 파라미터 조합, 교차검증할 수)
grid = GridSearchCV(tree_reg, params, cv=5)
grid.fit(X_train, y_train)
#가장 좋은 조합
grid.best_params_
#가장 좋을 조합일 때의 정확도
grid.best_score_✅ SVM모델(Support Vector Machines) : model은 SV에서 가장 멀리!

- 선 세개가 모두 정확히 분류를 해낸 모습.
- 그리는 것에 따라 무수히 많은 선이 그어질 수 있는데
그 중 2번이 제일 분류를 잘한 것 같다.- 애매한 부분을 제일 판단을 잘 할 수 있는 선이기 때문
- 기울기가 많이 기울은 3번 선은 선과 데이터가 가까워 정확도가 높을 것 같지만
더 많은 데이터를 넣었을 때, 과대적합이 일어나 실제 다른 데이터가 들어오면
다른 결과로 판단할 가능성이 높다.
- 2번선 경우에는 그룹과 가장 멀리 떨어져 SVM모델의 최적의 값이 된다.
- 1번 선과 3번선은 기울기가 문제가 아닌
결과값들과 가까이 붙어있기 때문에
데이터가 조금만 달라져도 다르게 예측을 할 수 있기 때문이다.
- 1번 선과 3번선은 기울기가 문제가 아닌
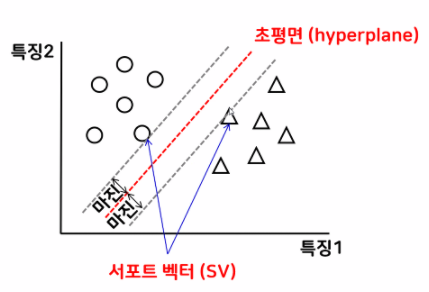
- SVC : 분류에 쓰이는 SVM
SVR : 회귀에 쓰이는 SVM - 각 클래스의 가장 바깥쪽 경계선을 긋고 해당 경계선에서 가장 먼(=마진이 큰) 선을 긋는다
- 결정 경계를 구분짓는 집단 경계값은 Support Vector라 한다.
- 데이터들에서 가장 멀리 떨어진 선이 SVM모델의 가장 정확한 모델

- SVC 모델에서 데이터가 자기 나와바리를 주장할때
데이터가 본인의 영역을 설정하려해서 영역에 따라 과대적합이 되면서 모델(=선)이 뒤틀리게 된다.
이는 규제 강도(C)로 조절한다. - 데이터 포인트들이 얼마나 자기의 영역을 주장하냐에 따라 선이 꼬이게 됨
선이 복잡해질수록 과대적합이 된다. - 하이퍼파라마터로 C와 gamma를 어떻게 정하느냐에 따라 모델의 정확도가 달라짐
- C : 값이 작을수록 규제가 강해짐.
- 어느정도의 이상치를 허용할 것인가? & 마진값을 얼마나 줄것인가? 를 결정한다.
- 얼마나 데이터를 정확하게 구분해낼것인가?
- C가 커질수록 마진이 줄어드는것을 알 수 있음.
- gamma : 데이터가 얼마나 나와바리가 크냐의 정도
- 얼마나 데이터에 boundary를 줄것인가?
- C : 값이 작을수록 규제가 강해짐.
'코딩공부 > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [스마트인재개발원] 활성화 함수와 교차 엔트로피 (0) | 2021.12.20 |
|---|---|
| [스마트인재개발원] 딥러닝 - 개요 (0) | 2021.12.17 |
| [스마트인재개발원] 머신러닝 - 앙상블 모델_Voting, Stacking, Bagging, Boosting (0) | 2021.12.11 |
| [스마트인재개발원] 머신러닝 - 정규화 (0) | 2021.12.09 |
| [스마트인재개발원]머신러닝 - 교차검증 (0) | 2021.12.08 |
Comments




