Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 하이퍼파라미터튜닝
- randomForest
- 오픈소스깃허브사용
- 활성화함수
- MSE
- 손실함수
- 취업성공패키지
- 안드로이드
- 2차프로젝트
- 비스포크시네마
- 국비지원
- KNN모델
- 취업연계
- JSP/Servlet
- 프로젝트
- 내일배움카드
- 스마트인재개발원
- intent
- 머신러닝
- 선형모델 분류
- 1차프로젝트
- 백엔드
- gitclone
- 2차 실전프로젝트
- ERD
- 교차검증
- semantic_segmentation
- MVCmodel
- springSTS
- 크롤링
Archives
- Today
- Total
또자의 코딩교실
[스마트인재개발원] 활성화 함수와 교차 엔트로피 본문

activation(활성화함수) - 자극에 대한 반응여부를 결정하는 함수
✅ 문제 유형에 따라 사용되는 활성화 함수와 오차함수 종류
| 문제 유형 | 출력층 활성화 함수 | 오차함수 |
| 회귀 | linear | mean_squared_error |
| 이진 분류 | sigmoid | binary_crossentropy |
| 다중 분류 | softmax | categorical_crossentropy |
- 이진분류는 Sigmoid함수를 사용(0과 1로 분류)
(0.5를 기준으로 높고 낮은지에 대한 확률 정보를 바탕으로 최종 출력을 결정함)- 입력층에서 sigmoid함수는 기울기 손실이라는 단점이 발생함
- softmax = 입력받은 값을 출력으로 0~1사이의 값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가진 함수
✅ Back Propagation (오차 역전파) 현상이란?

= 다층 퍼셉트론에서의 최적화 과정
결괏괎의 오차를 구해 이를 토대로 하나 앞선 가중치를 차례로 거슬러 올라가며 조정해감.
- 오차 역전파 구동방식
- 임의의 초기 가중치를 준뒤 결괏값을 계산
- 계산 결과와 우리가 원하는 값 사이의 오차를 구함
- 경사하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트함
- 위 과정을 오차가 줄어들지 않을 때 까지 반복함 (=미분값이 0에 가까워지는 방향으로 나아감)
- 시그모이드 함수를 미분하면 최대치가 0.3이다. 1보다 작으므로 계속 곱하다보면 0에 가까워짐. 따라서 여러 층을 거칠 수록 기울기가 사라져 가중치를 수정하기가 어려워짐. (=기울기 소실현상 발생!)
✅ Gradient Vanish (기울기 소실) 현상이란?

= 오차 역전파에 따라 학습을 진행했을 때 여러 퍼셉트론에서 계속해서 0부터 1사이의 결과값을 출력하는 시그모이드를 사용하면
여러번 작은 결과값이 곱해지며 입력값이 적어지게 된다.
- 따라서 특성이 작아지고 결과값을 출력하기도 힘들어짐.
- 멀티 레이어 퍼셉트론에서 시그모이드를 사용하게 되면 값이 점점 작아져서 효과가 없음.
따라서 이 문제를 해결하기 위한 활성화 함수들의 개선노력이 재고됨.
✅ 활성화 함수의 개선과정과 개선된 활성화 함수들
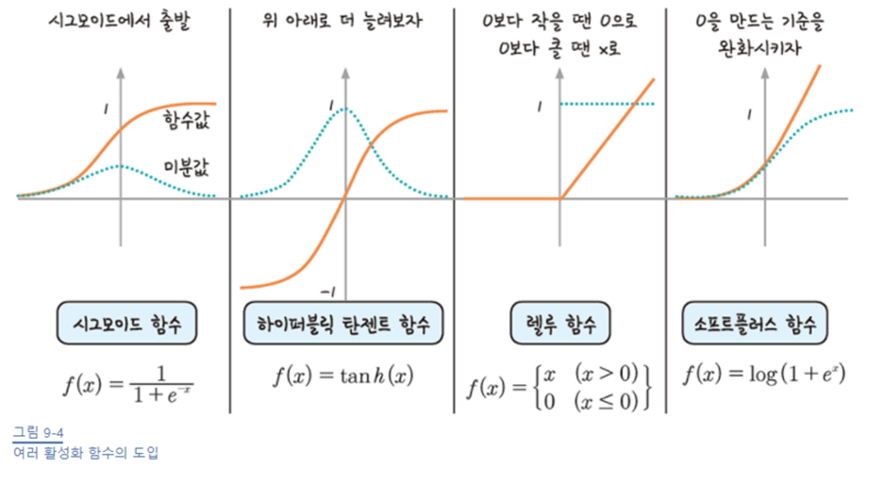

- sigmoid = 이진분류 문제에 사용 (0부터 0.3까지의 값) >> 기울기 소실 존재
- tanh = 위 아래로 더 늘려보자. (0부터 1까지의 값) >> 기울기 소실 존재
- ReLU = 0보다 작을 땐 0으로 밀어버리고, 0보다 클 땐 x로
ReLU 의 업그레이드 함수들.
더 나은 판단을 할 수 있다는 장점이 있지만 굉장히 계산량이 많아지고
큰 변화또한 일어나지 않아 대체적으로 ReLU를 사용하고 있다.
- Leaky ReLU = ReLU에서 0인 값을 활용해보자. 아주작은 값이라도 0인 값들을 0으로 밀지 말고 남겨보자.
- Maxout = ReLU + Leaky ReLU (두개 짬뽕을 시켜보자)
- ELU = 0이하의 값을 아주아주아주 작은 값으로 사용해보되 0에 가까운 유의미한 분류 값을 많이 사용해보자.
- softplus = 0을 만드는 기준을 완화시키자
✅ 오차 함수 (손실함수) (평균 제곱계열, 교차 엔트로피 계열)
케라스에서 사용되는 대표적인 오차 함수
| 평균 제곱 계열 | mean_squared_error | 평균 제곱 오차 |
| mean_absolute_error | 평균 절대 오차 (실제 값과 예측 값 차이의 절댓값 평균) |
|
| mean_absolute_percentage_error | 평균 절대 백분율 오차 (절댓값 오차를 절댓값으로 나눈 후 평균) |
|
| mean_squared_logarithmic_error | 평균 제곱 로그 오차 (실제 값과 예측 값에 로그를 적용한 값의 차이를 제곱한 값의 평균) |
|
| 교차 엔트로피 계열 | categorical_crossentropy | 범주형 교차 엔트로피 오차(일반적인 분류) |
| binary_crossentropy | 이항 교차 엔트로피 오차 (이진분류 예측할 때) |
교차 엔트로피는 주로 분류 문제에서 많이 사용되는데, 특별히 예측 값이 참과 거짓 둘 중 하나인 형식일 때는 binary_crossentropy (이항 교차 엔트로피) 를 쓴다.
출처: 모두의 딥러닝 - 133p
'코딩공부 > 머신러닝 & 딥러닝' 카테고리의 다른 글
| [스마트인재개발원] 딥러닝 - 개요 (0) | 2021.12.17 |
|---|---|
| [스마트 인재개발원] Linear Model(선형 회귀모델)과 선형모델 평가요소 (0) | 2021.12.13 |
| [스마트인재개발원] 머신러닝 - 앙상블 모델_Voting, Stacking, Bagging, Boosting (0) | 2021.12.11 |
| [스마트인재개발원] 머신러닝 - 정규화 (0) | 2021.12.09 |
| [스마트인재개발원]머신러닝 - 교차검증 (0) | 2021.12.08 |
Comments




